Unveiling The Power Of Karnaugh Maps: A Comprehensive Guide To Their Applications

Unveiling the Power of Karnaugh Maps: A Comprehensive Guide to Their Applications

Related Articles: Unveiling the Power of Karnaugh Maps: A Comprehensive Guide to Their Applications

Introduction

With enthusiasm, let’s navigate through the intriguing topic related to Unveiling the Power of Karnaugh Maps: A Comprehensive Guide to Their Applications. Let’s weave interesting information and offer fresh perspectives to the readers.

Unveiling the Power of Karnaugh Maps: A Comprehensive Guide to Their Applications

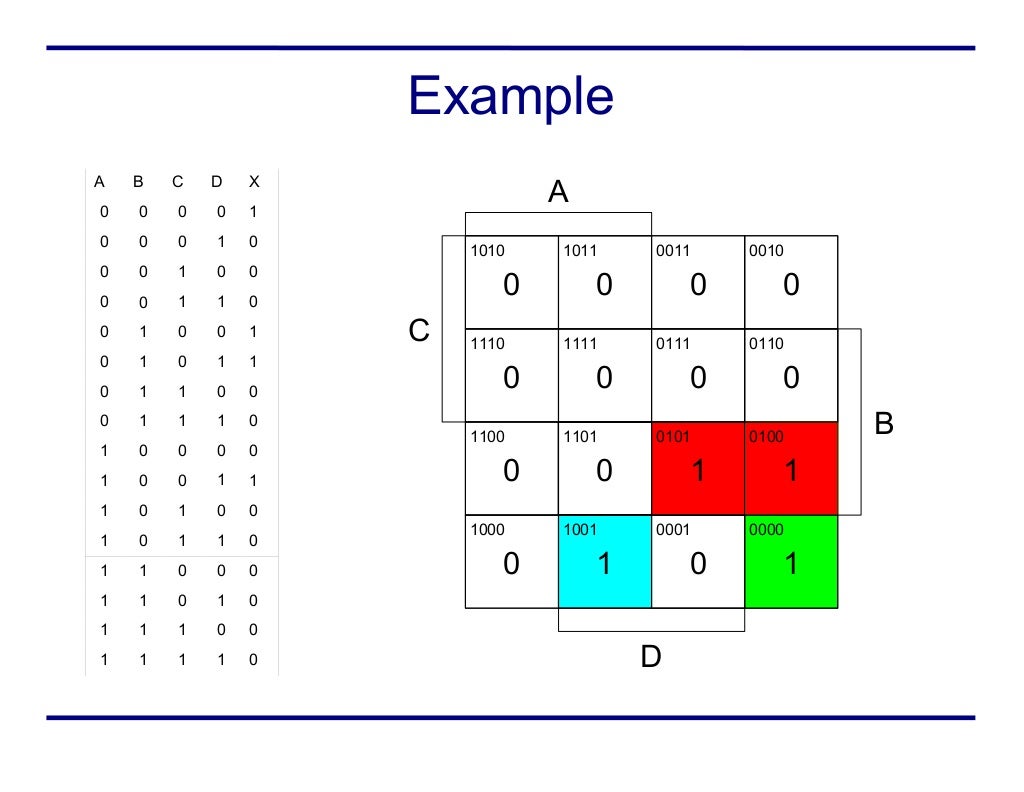
Karnaugh maps, often referred to as K-maps, are a visual tool used in logic design to simplify Boolean expressions and minimize the number of logic gates required for a given function. This simplification process leads to more efficient, cost-effective, and reliable digital circuits. K-maps offer a systematic and intuitive approach to Boolean algebra, enabling designers to visualize and manipulate logic functions with ease.

Understanding the Foundation: Karnaugh Maps Explained

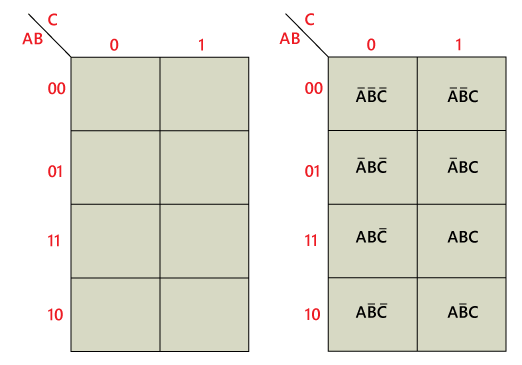
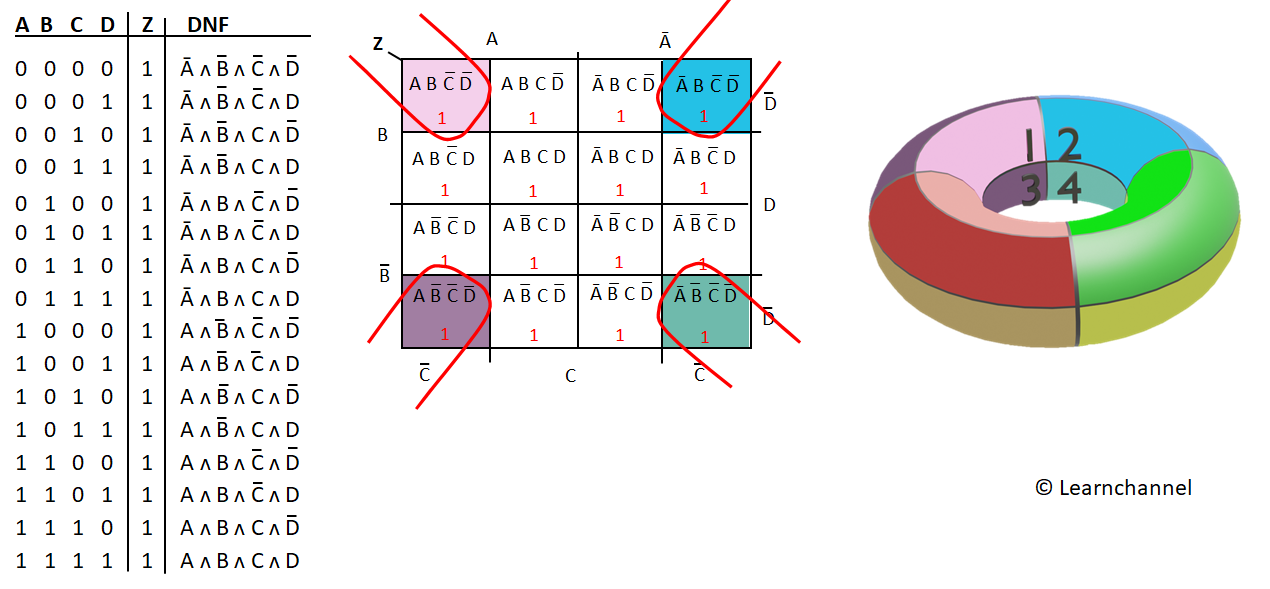
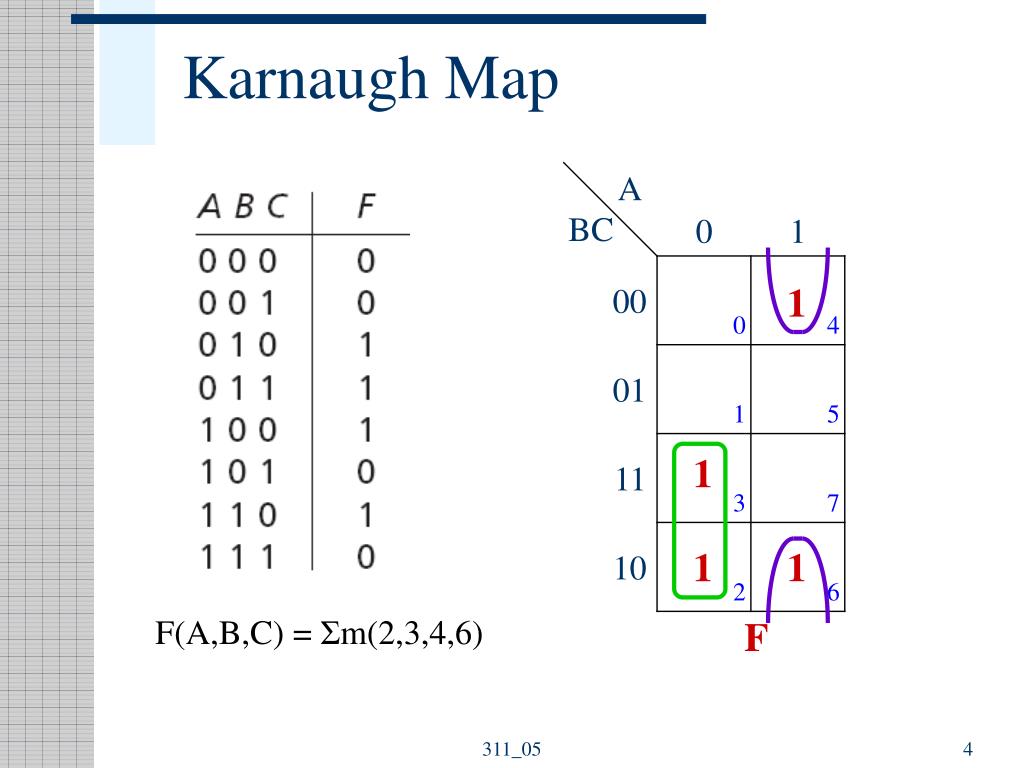
A K-map is a graphical representation of a truth table, where each cell represents a unique combination of input variables. The arrangement of cells is crucial, ensuring adjacent cells differ by only one variable. This arrangement facilitates the identification of groups of adjacent ‘1’ cells, which correspond to simplified terms in the Boolean expression.

Applications of Karnaugh Maps in Digital Logic Design

K-maps find widespread applications in various aspects of digital logic design, including:

1. Minimization of Boolean Expressions:

• Simplifying Circuit Design: K-maps help identify redundant terms and eliminate unnecessary logic gates, resulting in a simpler and more efficient circuit. This simplification reduces the number of components, lowers power consumption, and enhances circuit performance.
• Cost Reduction: Minimizing logic gates directly translates to lower manufacturing costs, as fewer components are required. This is particularly significant in large-scale integrated circuits (ICs), where even minor reductions in complexity can lead to significant savings.
• Improved Reliability: Simplified circuits are less prone to errors and malfunctions due to fewer interconnections and components. This increased reliability is crucial for applications where dependability is paramount, such as aerospace and medical devices.

2. Logic Function Implementation:

• Direct Synthesis from Truth Tables: K-maps allow for the direct translation of truth tables into minimized Boolean expressions, simplifying the design process. This eliminates the need for manual manipulation of Boolean equations, leading to faster and more accurate circuit implementation.
• Versatile Application: K-maps can handle various types of logic functions, including sum-of-products (SOP), product-of-sums (POS), and exclusive-OR (XOR) expressions. This versatility makes them a valuable tool for a wide range of digital design tasks.

3. Design of Combinational Circuits:

• Optimizing Logic Circuits: K-maps are instrumental in optimizing combinational circuits, which produce outputs based solely on the current inputs. By minimizing the Boolean expressions, K-maps ensure the use of the fewest logic gates, leading to more compact and efficient circuits.
• Designing Multiplexers and Decoders: K-maps are used extensively in the design of multiplexers and decoders, crucial components in digital systems. By simplifying the logic functions involved, K-maps contribute to the efficient implementation of these essential building blocks.

4. Design of Sequential Circuits:

• State Machine Minimization: K-maps can be used to minimize the number of states in a state machine, a fundamental component in sequential circuits. This simplification reduces the complexity of the circuit and improves its performance.
• Optimizing State Transitions: K-maps help identify optimal state transitions, ensuring the efficient flow of information within a sequential circuit. This optimization enhances the circuit’s speed and accuracy.

5. Error Detection and Correction:

• Parity Generation and Checking: K-maps are used in the design of parity circuits, which add redundant bits to data to detect and correct errors during transmission. This ensures data integrity and reliability, particularly in communication systems.
• Hamming Code Implementation: K-maps assist in the implementation of Hamming codes, a powerful error correction technique used in data storage and transmission. These codes provide robust error detection and correction capabilities, crucial for maintaining data integrity.

FAQs on Karnaugh Maps:

Q1: What are the limitations of Karnaugh maps?

• Complexity: K-maps become increasingly complex and difficult to use for functions with a large number of input variables (more than five or six).
• Difficult for Non-Standard Functions: Functions with complex logic structures or non-standard forms may not be easily represented or simplified using K-maps.

Q2: Are there alternatives to Karnaugh maps?

• Quine-McCluskey Algorithm: This algebraic method provides a more systematic approach to Boolean minimization, suitable for functions with a higher number of variables.
• Computer-Aided Design (CAD) Tools: Modern CAD tools offer automated minimization algorithms that can handle complex Boolean expressions, providing a more efficient alternative for large-scale designs.

Q3: How do I choose between using K-maps and other methods?

• Complexity of the Function: For functions with up to four or five variables, K-maps are a convenient and efficient tool.
• Design Complexity: For large-scale designs or complex logic functions, automated methods and CAD tools are often more suitable.

Tips for Using Karnaugh Maps Effectively:

• Choose the Right Map Size: Select a K-map with a number of cells corresponding to the number of input variables.
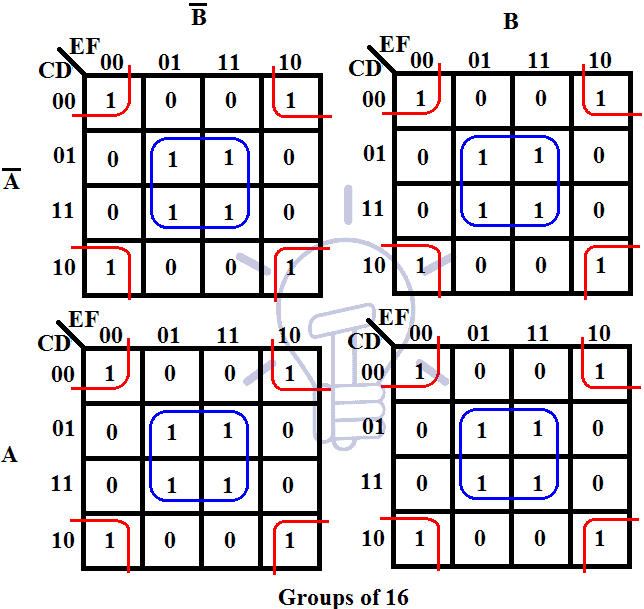
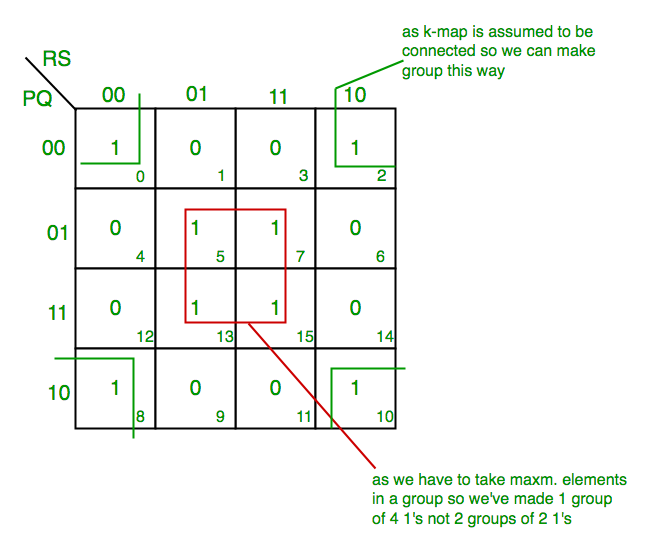
• Identify Groups of Adjacent ‘1’s: Look for groups of ‘1’s that are adjacent, including those that wrap around the edges of the map.
• Prioritize Larger Groups: Larger groups represent simpler terms, leading to more efficient circuits.
• Use Don’t Care Conditions: ‘Don’t care’ conditions, denoted by ‘X’, can be used to further simplify the expression.

Conclusion:

Karnaugh maps remain a valuable tool for logic designers, offering a visual and intuitive approach to simplifying Boolean expressions. They are particularly effective for small to medium-sized functions and provide a solid foundation for understanding logic minimization principles. While automated tools and alternative methods have emerged for larger-scale designs, K-maps continue to be an essential tool for teaching and understanding the fundamentals of digital logic design. Their ability to simplify complex expressions and optimize circuit implementations makes them a cornerstone of digital system design, contributing to the creation of efficient, reliable, and cost-effective circuits.

Closure

Thus, we hope this article has provided valuable insights into Unveiling the Power of Karnaugh Maps: A Comprehensive Guide to Their Applications. We hope you find this article informative and beneficial. See you in our next article!