Unlocking the Power of Simplification: A Comprehensive Guide to Karnaugh Maps
Related Articles: Unlocking the Power of Simplification: A Comprehensive Guide to Karnaugh Maps
Introduction
With great pleasure, we will explore the intriguing topic related to Unlocking the Power of Simplification: A Comprehensive Guide to Karnaugh Maps. Let’s weave interesting information and offer fresh perspectives to the readers.
Table of Content
Unlocking the Power of Simplification: A Comprehensive Guide to Karnaugh Maps

The realm of digital circuit design hinges on the ability to express complex logical functions in a manner both efficient and comprehensible. This is where the Karnaugh map, a visual tool developed by Maurice Karnaugh in 1953, shines. It provides a systematic and intuitive approach to simplifying Boolean expressions, leading to optimized circuits with reduced component count, lower power consumption, and enhanced reliability.
Understanding the Fundamentals
At its core, a Karnaugh map is a graphical representation of a truth table, where each cell corresponds to a unique combination of input variables. The map’s arrangement follows a specific pattern, ensuring adjacent cells differ by only a single variable. This seemingly simple arrangement holds the key to efficient Boolean expression simplification.
The Power of Adjacency
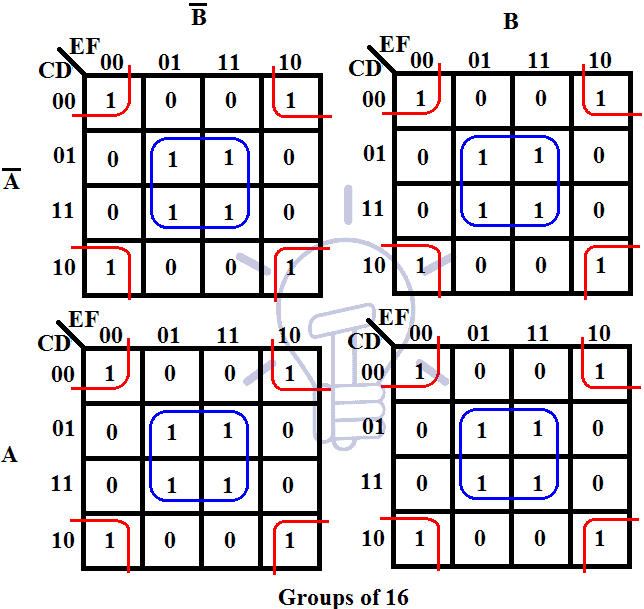
The magic of Karnaugh maps lies in the concept of "adjacent" cells. When two adjacent cells contain a "1" (representing a true output), they can be grouped together, signifying a common term in the Boolean expression. This grouping process, known as "looping," allows for the identification of minimal sum-of-products (SOP) or product-of-sums (POS) expressions.
A Step-by-Step Guide to Mapping
Let’s consider a simple example to illustrate the process:
Scenario: Design a circuit that outputs a "1" when exactly two out of three inputs (A, B, and C) are "1."
- Truth Table: Begin by constructing a truth table for the given function.
| A | B | C | Output |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 0 |
- Karnaugh Map: Create a Karnaugh map with rows and columns representing the input variables. The map’s arrangement ensures adjacent cells differ in only one variable.
| 00 | 01 | 11 | 10 | |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 | 1 |
-
Mapping the Outputs: Fill in the map with the output values from the truth table, aligning each cell with its corresponding input combination.
-
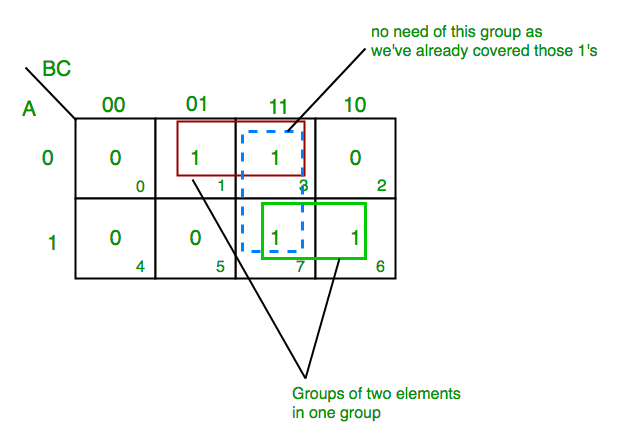
Looping: Identify adjacent cells containing "1" and group them together, forming rectangular loops. These loops should be as large as possible, encompassing the maximum number of "1"s.
In our example, there are three groups of two "1"s:
- One group in the bottom row (10, 11)
- One group in the rightmost column (01, 11)
- One group in the middle columns (01, 10)
- Boolean Expression: Each loop represents a term in the minimized Boolean expression. The term is formed by identifying the input variables that remain constant within the loop.
- The bottom row loop yields the term
BC', whereC'represents the complement of C. - The rightmost column loop yields
AB'. - The middle column loop yields
A'B.
Therefore, the simplified Boolean expression for the given function is:
F = BC' + AB' + A'B
Beyond Basic Application: Expanding the Scope
Karnaugh maps are not limited to simple Boolean expressions. They are versatile tools with numerous applications in digital circuit design, including:
- Multi-Level Logic Simplification: Karnaugh maps can be applied to simplify multi-level logic expressions, where outputs depend on intermediate logic functions.
- Don’t-Care Conditions: In some cases, certain input combinations may not be relevant or have undefined outputs. Karnaugh maps allow for the inclusion of "don’t-care" conditions, further optimizing the simplification process.
- State Machine Design: Karnaugh maps can be used to simplify state transition tables in sequential circuits, leading to efficient state machine implementations.
- Error Detection and Correction: By analyzing the relationships between input and output variables, Karnaugh maps can aid in the design of circuits with error detection and correction capabilities.
FAQs on Karnaugh Maps
Q: What is the maximum number of variables a Karnaugh map can handle?
A: The number of variables a Karnaugh map can handle is limited by its size. A 2-variable map has 4 cells, a 3-variable map has 8 cells, a 4-variable map has 16 cells, and so on. For larger numbers of variables, other simplification methods, like the Quine-McCluskey algorithm, become more practical.
Q: Can Karnaugh maps handle functions with multiple outputs?
A: While Karnaugh maps are primarily designed for single-output functions, they can be extended to handle multiple outputs by creating separate maps for each output.
Q: What are the advantages of using Karnaugh maps over other simplification methods?
A: Karnaugh maps provide a visual and intuitive approach to simplification, making it easier to understand the logic behind the minimized expression. They are particularly well-suited for small-scale problems with up to four variables.
Tips for Effective Karnaugh Map Usage
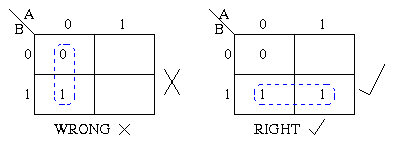
- Understanding Adjacency: Pay close attention to the arrangement of cells and ensure you correctly identify adjacent cells for looping.
- Looping Strategies: Aim to form the largest possible loops, encompassing the maximum number of "1"s.
- Don’t-Care Conditions: Utilize "don’t-care" conditions strategically to further simplify expressions.
- Practice: The best way to master Karnaugh maps is through practice. Work through various examples to gain familiarity with the process.
Conclusion
Karnaugh maps, with their intuitive visual representation and systematic approach, remain a powerful tool for simplifying Boolean expressions. They are essential for efficient digital circuit design, leading to optimized circuits with reduced complexity, lower power consumption, and enhanced reliability. While other simplification methods exist, Karnaugh maps provide a valuable visual aid, particularly for small-scale problems, fostering a deeper understanding of logic function simplification. By mastering the art of Karnaugh map usage, designers can unlock the power of simplification and create robust, efficient digital circuits.





Closure
Thus, we hope this article has provided valuable insights into Unlocking the Power of Simplification: A Comprehensive Guide to Karnaugh Maps. We hope you find this article informative and beneficial. See you in our next article!