The Power Of Simplification: Karnaugh Maps In Digital Design

The Power of Simplification: Karnaugh Maps in Digital Design

Related Articles: The Power of Simplification: Karnaugh Maps in Digital Design

Introduction

With enthusiasm, let’s navigate through the intriguing topic related to The Power of Simplification: Karnaugh Maps in Digital Design. Let’s weave interesting information and offer fresh perspectives to the readers.

The Power of Simplification: Karnaugh Maps in Digital Design

The realm of digital design thrives on the ability to manipulate and optimize complex Boolean expressions. One tool that stands out for its visual and intuitive approach to simplification is the Karnaugh map (K-map). Developed by Maurice Karnaugh in 1953, this graphical representation of Boolean functions has proven invaluable in reducing circuit complexity, minimizing cost, and enhancing performance.

Understanding the Essence of K-Maps

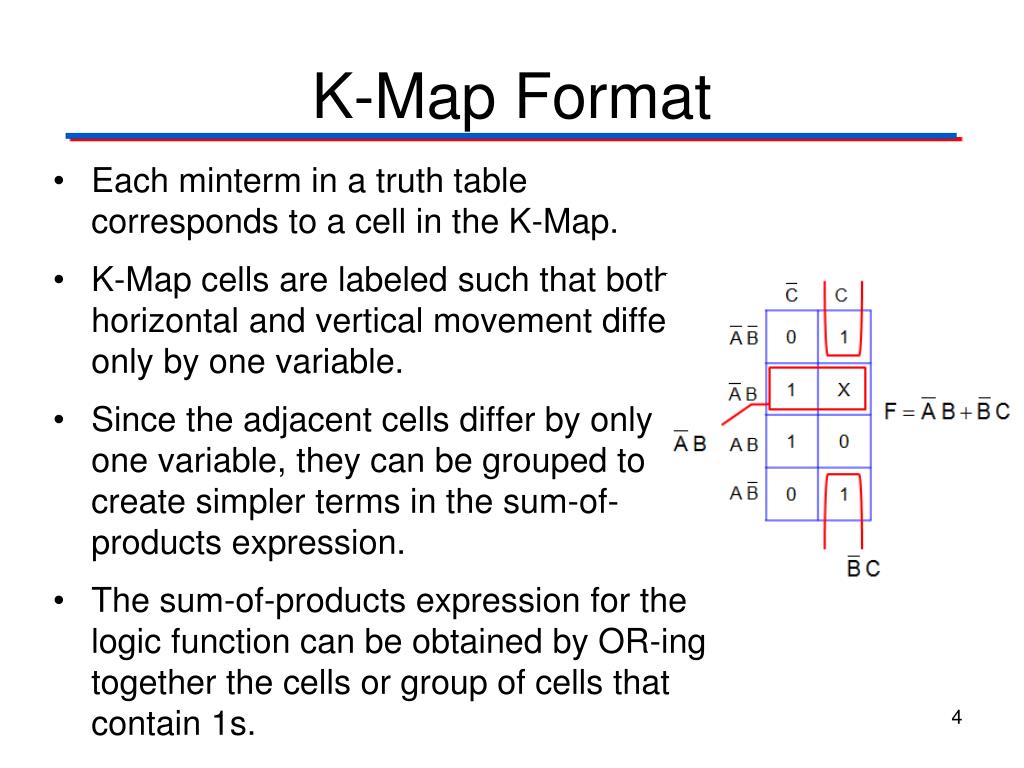
At its core, a K-map is a graphical representation of a truth table, a tabular listing of all possible input combinations and their corresponding outputs for a Boolean function. K-maps employ a grid structure, where each cell represents a unique combination of input variables. The arrangement of cells is not arbitrary; it ensures that adjacent cells differ in only one input variable, facilitating the identification of adjacent groups of ‘1’s. These groups, known as ‘implicants,’ represent simplified terms in the Boolean expression.

Constructing a K-Map: A Step-by-Step Approach

1. Identify the number of input variables: The number of input variables dictates the size of the K-map. A two-variable function requires a 2×2 grid, a three-variable function a 2×4 grid, a four-variable function a 4×4 grid, and so on.

2. Assign binary values to the rows and columns: Each row and column represents a unique combination of input variables. Binary values are assigned in a Gray code sequence, where each consecutive value differs by only one bit. This ensures that adjacent cells differ in only one variable.

3. Populate the K-map with output values: The output value for each input combination is entered in the corresponding cell. A ‘1’ represents a ‘true’ output, and a ‘0’ represents a ‘false’ output.

Simplifying Boolean Expressions with K-Maps

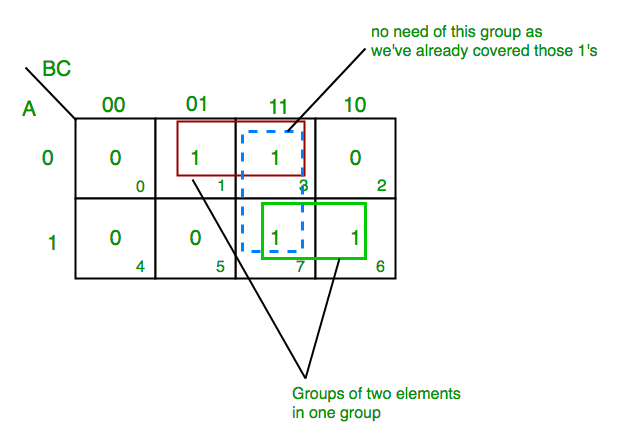
The true power of K-maps lies in their ability to visually simplify complex Boolean expressions. This simplification is achieved by identifying and grouping adjacent cells containing ‘1’s. The following rules govern the grouping process:

• Groups must be rectangular: Groups can be horizontal, vertical, or diagonal, but must have sides that are powers of two.
• Groups must be as large as possible: Larger groups represent simpler terms.
• Groups can overlap: Overlapping groups are allowed, as they contribute to multiple terms.
• All ‘1’s must be covered: Each cell containing a ‘1’ must be included in at least one group.

Once the groups are identified, the simplified Boolean expression is obtained by writing down the sum of terms, where each term corresponds to a group. The term for a group is formed by identifying the variables that are constant within the group and setting them to their respective values.

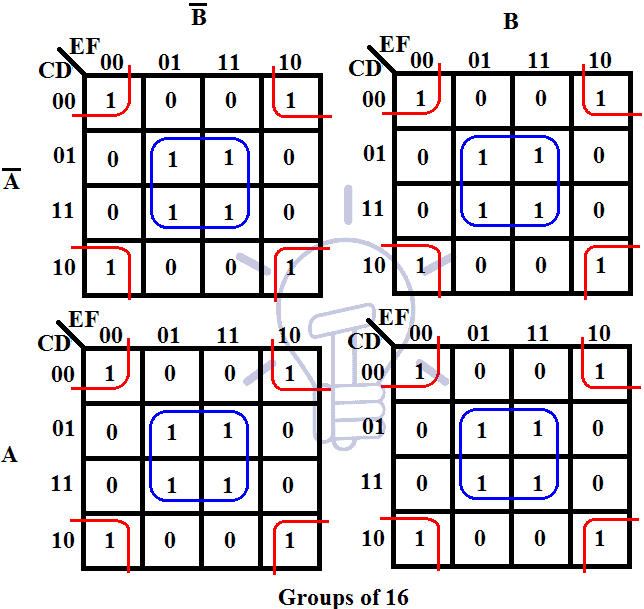
Illustrative Example: Simplifying a Four-Variable Function

Consider the following Boolean function:

F(A, B, C, D) = Σ(0, 1, 2, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15)

To simplify this function using a K-map:

1. Create a 4×4 K-map: The function has four input variables, so a 4×4 grid is required.

2. Assign binary values to the rows and columns: The rows and columns are assigned Gray code values for A, B, C, and D respectively.

3. Populate the K-map: Enter ‘1’s in the cells corresponding to the minterms listed in the function’s sum-of-products form (Σ).

4. Identify groups: The K-map reveals several groups: one group of 16 ‘1’s, covering the entire map, and one group of 8 ‘1’s, covering the rightmost column.

5. Write the simplified expression: The group of 16 ‘1’s corresponds to the term ‘1’ (since all variables are constant within the group), and the group of 8 ‘1’s corresponds to the term ‘D’ (as D is the only variable that is constant within the group).

Therefore, the simplified expression for F(A, B, C, D) is: F(A, B, C, D) = 1 + D

Benefits of Using K-Maps

• Simplified Boolean Expressions: K-maps provide a visual and intuitive method for identifying and grouping adjacent ‘1’s, leading to simplified Boolean expressions.
• Reduced Circuit Complexity: Simplified expressions translate into fewer logic gates in the circuit, reducing complexity and cost.
• Improved Performance: Reduced complexity leads to faster circuit operation and improved power efficiency.
• Enhanced Design Flexibility: K-maps enable designers to explore different simplification options, leading to more efficient and optimized designs.

Applications of K-Maps in Digital Design

K-maps find widespread use in various digital design applications, including:

• Logic Circuit Design: Simplifying Boolean expressions for logic circuits, leading to reduced gate count and improved performance.
• Digital System Design: Optimizing digital systems, such as memory systems, arithmetic logic units (ALUs), and control units.
• Combinational Circuit Design: Designing circuits that produce an output based solely on the current input values, such as decoders, encoders, and multiplexers.
• Sequential Circuit Design: Designing circuits that produce an output based on both the current input and the past state of the circuit, such as flip-flops, registers, and counters.

FAQs on K-Maps

Q1: Can K-maps be used for functions with more than four input variables?

A: While K-maps are most effective for functions with up to four variables, they become cumbersome for functions with five or more variables. For such functions, alternative simplification techniques, like the Quine-McCluskey method, are typically employed.

Q2: What if the K-map has isolated ‘1’s that cannot be grouped?

A: Isolated ‘1’s represent individual terms in the simplified expression. They cannot be grouped and contribute to the overall expression as individual minterms.

Q3: How do K-maps handle don’t care conditions?

A: Don’t care conditions, represented by ‘X’s in the K-map, provide flexibility in grouping. They can be treated as either ‘0’ or ‘1’ depending on which grouping leads to the most simplified expression.

Tips for Using K-Maps Effectively

• Start with a clear understanding of the Boolean function: Carefully analyze the truth table or the sum-of-products form of the function before constructing the K-map.
• Choose the appropriate size for the K-map: Select the grid size that corresponds to the number of input variables.
• Use Gray code for row and column assignments: This ensures that adjacent cells differ in only one variable.
• Look for the largest possible groups: Larger groups lead to simpler terms.
• Don’t forget to cover all ‘1’s: Each cell containing a ‘1’ must be included in at least one group.
• Consider don’t care conditions: Use them strategically to simplify the expression.
• Verify the simplified expression: Test the simplified expression against the original function to ensure correctness.

Conclusion

Karnaugh maps provide a powerful and intuitive method for simplifying Boolean expressions, reducing circuit complexity, and enhancing performance. Their visual nature and straightforward grouping rules make them a valuable tool for digital designers. While alternative simplification methods exist for functions with more variables, K-maps remain a cornerstone of digital design, empowering engineers to optimize circuits and create efficient and effective digital systems.

Closure

Thus, we hope this article has provided valuable insights into The Power of Simplification: Karnaugh Maps in Digital Design. We hope you find this article informative and beneficial. See you in our next article!