The Power of Simplification: Applications of Karnaugh Maps in Digital Design
Related Articles: The Power of Simplification: Applications of Karnaugh Maps in Digital Design
Introduction
With great pleasure, we will explore the intriguing topic related to The Power of Simplification: Applications of Karnaugh Maps in Digital Design. Let’s weave interesting information and offer fresh perspectives to the readers.
Table of Content
The Power of Simplification: Applications of Karnaugh Maps in Digital Design

Karnaugh maps, often referred to as K-maps, are a valuable tool in the realm of digital logic design. Their primary function is to simplify Boolean expressions, a process crucial for creating efficient and cost-effective digital circuits. This simplification, achieved through the visual representation of Boolean functions, translates into smaller, faster, and more reliable circuits.
Understanding the Basics:
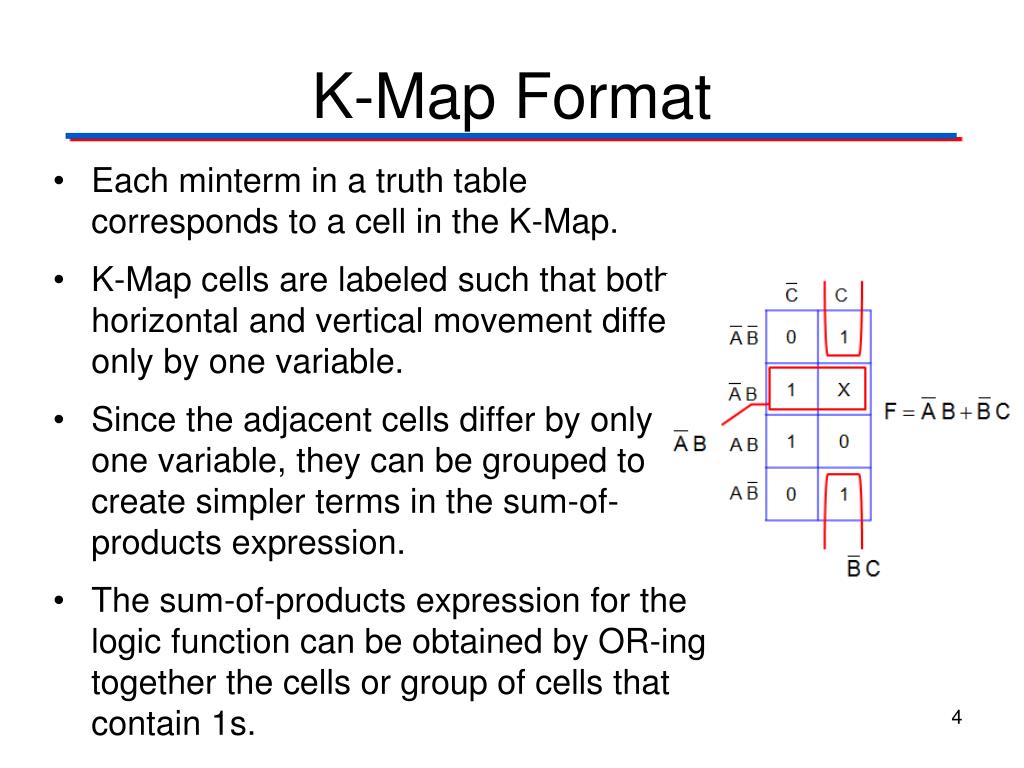
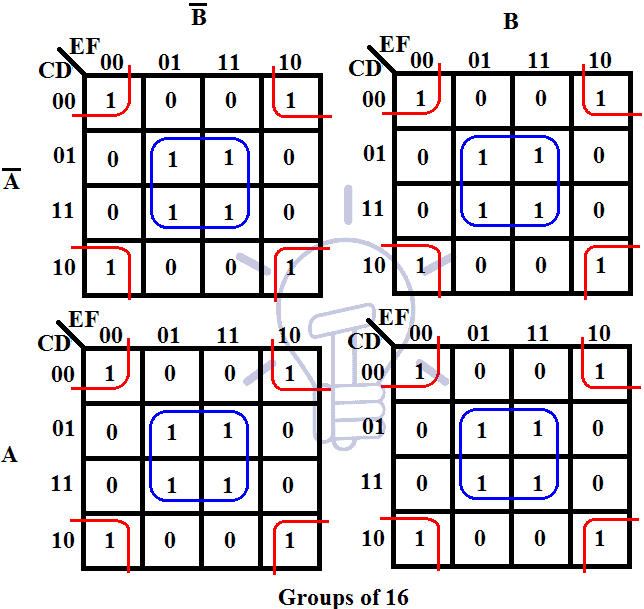
K-maps are essentially graphical representations of truth tables, providing a visual method for identifying and grouping together adjacent minterms (product terms) that correspond to logical "1" outputs. Each cell within the map represents a unique combination of input variables, arranged in a specific order to facilitate easy identification of adjacent cells. The adjacency is not limited to horizontal or vertical neighbors but also includes cells that share an edge, even if they appear to be on opposite sides of the map.
Key Applications:
The power of K-maps lies in their ability to simplify complex Boolean expressions, leading to various applications in digital design:
1. Logic Circuit Minimization:
The most fundamental application of K-maps is the simplification of Boolean expressions. By identifying adjacent minterms with "1" values and grouping them into larger blocks, K-maps allow designers to express the same logic function using fewer logic gates. This results in smaller, less complex circuits, leading to reduced costs, improved performance, and lower power consumption.
2. Design of Combinational Circuits:
Combinational circuits, whose outputs depend solely on their current inputs, are widely used in digital systems. K-maps play a crucial role in designing these circuits by facilitating the derivation of minimal Boolean expressions from truth tables. This process involves identifying groups of adjacent minterms representing "1" outputs, leading to the generation of simplified logic equations for each output.
3. Design of Sequential Circuits:
While primarily used for combinational circuits, K-maps can also be applied in the design of sequential circuits, which have memory elements and whose outputs depend on both current and past inputs. In this context, K-maps are used to simplify the state transition logic, leading to more efficient and compact implementations of sequential circuits.
4. Boolean Algebra Verification:
K-maps provide a visual method for verifying the correctness of Boolean expressions. By representing the expression on a K-map and comparing it to the expected truth table, designers can quickly identify any discrepancies and ensure the logic function is accurately implemented.
5. Education and Training:
K-maps are a valuable teaching tool for introducing students to the fundamentals of Boolean algebra and digital logic design. Their visual nature allows students to grasp the concepts of simplification and manipulation of Boolean expressions in a more intuitive manner, facilitating a deeper understanding of the underlying principles.
Benefits of Using K-maps:
- Simplification: K-maps provide a systematic and efficient method for simplifying Boolean expressions, leading to more compact and cost-effective circuit designs.
- Visual Representation: The visual nature of K-maps allows for a more intuitive understanding of Boolean functions, making it easier to identify patterns and simplify expressions.
- Reduced Complexity: By simplifying logic expressions, K-maps reduce the complexity of digital circuits, leading to faster operation, lower power consumption, and improved reliability.
- Error Detection: K-maps aid in identifying errors in Boolean expressions by providing a visual representation that facilitates comparison with expected truth tables.
- Educational Value: K-maps serve as a valuable teaching tool for introducing students to the concepts of Boolean algebra and digital logic design.
FAQs:
Q: What are the limitations of K-maps?
A: K-maps are effective for simplifying Boolean expressions with a limited number of input variables (typically up to six). For larger expressions, alternative methods like Quine-McCluskey algorithm are required. Additionally, K-maps are not suitable for dealing with Boolean functions that have multiple outputs.
Q: Can K-maps be used for functions with multiple outputs?
A: While K-maps are primarily used for single-output functions, they can be extended to handle multiple outputs by creating a separate K-map for each output. However, this approach can become cumbersome for complex functions with many outputs.
Q: How does the arrangement of cells in a K-map affect its use?
A: The specific arrangement of cells in a K-map ensures that adjacent cells correspond to input combinations that differ by only one variable. This arrangement facilitates the identification of adjacent minterms, crucial for simplification.
Q: What is the relationship between K-maps and truth tables?
A: K-maps are essentially graphical representations of truth tables. Each cell in a K-map corresponds to a specific row in the truth table, representing a unique combination of input variables.
Q: Are there any other methods for simplifying Boolean expressions?
A: Yes, besides K-maps, other methods like the Quine-McCluskey algorithm and Espresso algorithm are used for simplifying Boolean expressions, particularly for functions with a larger number of input variables.
Tips for Using K-maps:
- Start with a truth table: Begin by creating a truth table for the desired Boolean function.
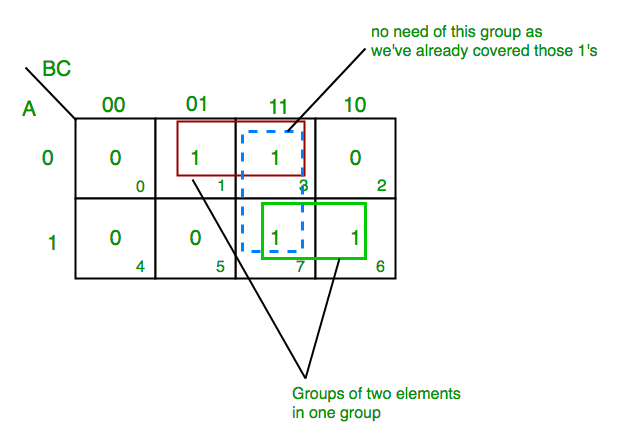
- Identify adjacent minterms: Look for groups of adjacent cells in the K-map that correspond to "1" outputs.
- Maximize group size: Aim to group the minterms into the largest possible blocks, including both horizontal and vertical adjacencies.
- Cover all "1" outputs: Ensure that all cells with "1" outputs are included in at least one group.
- Minimize the number of groups: Aim to simplify the expression using the fewest possible groups.
- Write the simplified expression: Based on the identified groups, write the simplified Boolean expression using the corresponding input variables.
Conclusion:
Karnaugh maps remain a powerful tool for simplifying Boolean expressions in digital logic design. Their visual nature and ability to identify adjacent minterms facilitate the creation of efficient and cost-effective circuits. While K-maps have limitations for functions with a large number of input variables, they continue to be an essential technique for understanding and manipulating Boolean expressions, particularly in educational settings. The ability to simplify logic expressions through K-maps remains crucial for designing digital circuits that are smaller, faster, and more reliable, ultimately contributing to the advancement of digital technology.





Closure
Thus, we hope this article has provided valuable insights into The Power of Simplification: Applications of Karnaugh Maps in Digital Design. We appreciate your attention to our article. See you in our next article!