The Enduring Relevance of Karnaugh Maps in Modern Digital Design
Related Articles: The Enduring Relevance of Karnaugh Maps in Modern Digital Design
Introduction
In this auspicious occasion, we are delighted to delve into the intriguing topic related to The Enduring Relevance of Karnaugh Maps in Modern Digital Design. Let’s weave interesting information and offer fresh perspectives to the readers.
Table of Content
The Enduring Relevance of Karnaugh Maps in Modern Digital Design

Karnaugh maps (K-maps), a graphical method for simplifying Boolean expressions, have been a cornerstone of digital design since their introduction in the 1950s. Despite the advent of sophisticated computer-aided design (CAD) tools, K-maps remain relevant and valuable in various aspects of digital circuit design and analysis. This article explores the enduring significance of K-maps in the modern context, examining their strengths, limitations, and areas of continued application.
Understanding the Essence of Karnaugh Maps
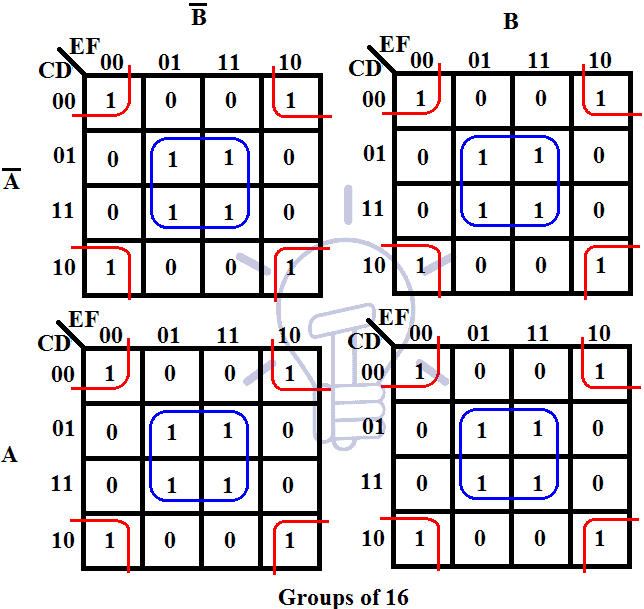
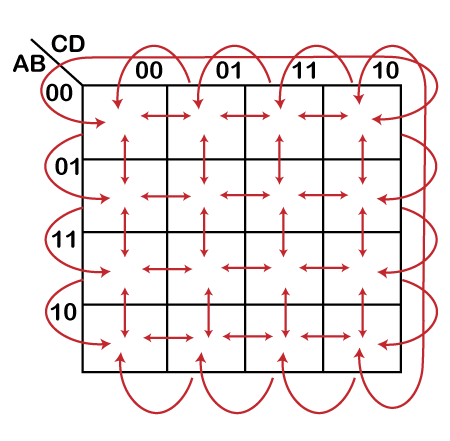
K-maps provide a visual representation of Boolean functions, simplifying the process of minimizing logical expressions. They utilize a grid structure where each cell corresponds to a unique combination of input variables. The values within the cells represent the output of the Boolean function for that specific input combination. By grouping adjacent cells containing ‘1’s (representing ‘true’ outputs), K-maps facilitate the identification of minimal sum-of-products (SOP) or product-of-sums (POS) expressions.
Advantages of Using Karnaugh Maps
-
Intuitive Visualization: K-maps offer a clear and intuitive visual representation of Boolean functions, making it easier to grasp the relationships between inputs and outputs. This visual approach aids in understanding the logic behind circuit design.
-
Simplification of Boolean Expressions: K-maps enable the simplification of complex Boolean expressions by identifying redundant terms and combining adjacent ‘1’s. This results in simpler and more efficient logic circuits.
-
Efficient Implementation: Simplified Boolean expressions derived from K-maps translate to fewer logic gates in the circuit implementation, reducing component count, power consumption, and cost.
-
Practical Learning Tool: K-maps serve as an excellent educational tool, providing a hands-on method for understanding Boolean algebra and logic design principles.
Limitations of Karnaugh Maps
-
Limited Scalability: K-maps become increasingly complex and challenging to use as the number of input variables increases. For functions with more than six variables, the graphical representation becomes cumbersome and less practical.
-
Manual Process: K-maps rely on manual manipulation and grouping of cells, which can be time-consuming and prone to errors, especially for larger and more complex circuits.
-
Limited Optimization: While K-maps effectively simplify Boolean expressions, they may not always yield the absolute minimum expression, especially for highly complex functions.
Applications of Karnaugh Maps in Modern Design
Despite their limitations, K-maps remain relevant and valuable in various aspects of modern digital design:
-
Educational Tool: K-maps continue to be widely used in education for teaching digital logic design principles and Boolean algebra. Their visual nature facilitates understanding and reinforces learning.
-
Small-Scale Circuit Design: For small-scale circuits with a limited number of input variables, K-maps provide a quick and efficient method for simplification and implementation.
-
Verification of CAD Results: K-maps can be used to verify the results of complex logic optimization performed by CAD tools. This manual verification helps ensure accuracy and provides a deeper understanding of the design process.
-
Understanding Logic Functions: K-maps offer a valuable tool for understanding the behavior of existing logic circuits by visualizing the relationships between inputs and outputs.
-
Logic Design for Specific Applications: In specialized applications where circuit simplicity and efficiency are paramount, K-maps can be used to optimize logic for specific requirements.
Frequently Asked Questions (FAQs)
Q: Can K-maps be used for circuits with more than six variables?
A: While K-maps are commonly used for up to six variables, their graphical representation becomes unwieldy for larger circuits. For circuits with more than six variables, alternative methods like Quine-McCluskey algorithm or computer-aided design tools are more suitable.
Q: Are K-maps still relevant in the age of CAD tools?
A: Yes, K-maps remain relevant, particularly for educational purposes, small-scale circuit design, verification of CAD results, and understanding existing logic functions. Their intuitive nature and ability to provide a deeper understanding of logic design principles make them valuable even with the availability of powerful CAD tools.
Q: What are some tips for using K-maps effectively?
A:
-
Start with a clear understanding of the Boolean function: Define the input variables, output function, and truth table before constructing the K-map.
-
Choose the appropriate K-map size: Select a K-map with the correct number of rows and columns based on the number of input variables.
-
Group adjacent ‘1’s: Identify and group adjacent cells containing ‘1’s, ensuring that each group has a power of 2 number of cells.
-
Write the simplified expression: Derive the simplified Boolean expression from the grouped cells, representing each group with a product term.
-
Verify the result: Double-check the simplified expression against the original Boolean function or truth table to ensure accuracy.
Conclusion
Karnaugh maps, despite their limitations, continue to hold a significant place in the realm of digital design. Their intuitive nature, ability to simplify Boolean expressions, and role as an effective educational tool make them an enduring and valuable resource for understanding and implementing logic circuits. While CAD tools have revolutionized the design process, K-maps remain relevant for specific applications, verification, and providing a deeper understanding of the underlying logic. Their enduring relevance underscores their importance in the evolution of digital design and their continued use in various aspects of the field.





Closure
Thus, we hope this article has provided valuable insights into The Enduring Relevance of Karnaugh Maps in Modern Digital Design. We hope you find this article informative and beneficial. See you in our next article!