Demystifying Karnaugh Maps: A Visual Approach To Boolean Logic Simplification

Demystifying Karnaugh Maps: A Visual Approach to Boolean Logic Simplification

Related Articles: Demystifying Karnaugh Maps: A Visual Approach to Boolean Logic Simplification

Introduction

With great pleasure, we will explore the intriguing topic related to Demystifying Karnaugh Maps: A Visual Approach to Boolean Logic Simplification. Let’s weave interesting information and offer fresh perspectives to the readers.

Demystifying Karnaugh Maps: A Visual Approach to Boolean Logic Simplification

Introduction

The realm of digital circuit design thrives on the efficient manipulation of Boolean expressions. These expressions, built from logical operators like AND, OR, and NOT, represent the behavior of digital circuits. However, as circuits grow in complexity, so do the Boolean expressions that describe them, leading to intricate and often cumbersome equations. This is where Karnaugh maps (K-maps) emerge as a powerful visualization tool, simplifying the process of minimizing Boolean expressions and optimizing circuit design.

Understanding the Essence of Karnaugh Maps

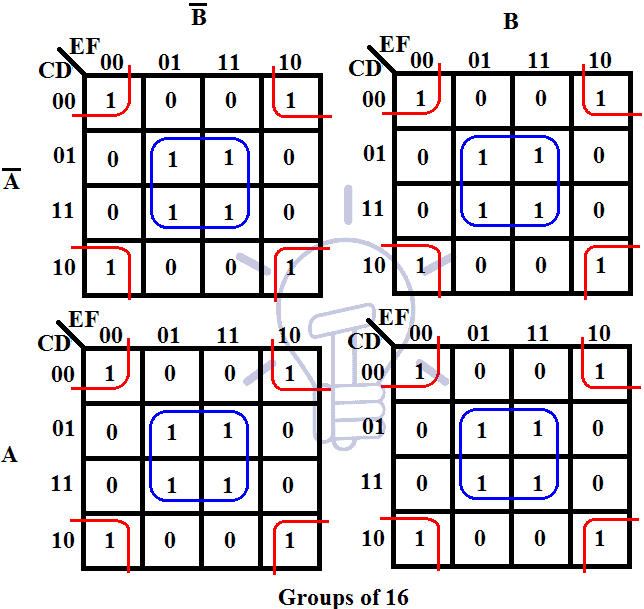
A Karnaugh map is a graphical representation of a Boolean function, providing a visual framework for simplifying Boolean expressions. It employs a grid structure where each cell corresponds to a unique combination of input variables. The map’s arrangement ensures that adjacent cells differ in only one input variable, enabling the identification of common terms and simplifying the function.

The Structure of a Karnaugh Map

K-maps are constructed based on the number of input variables in the Boolean function. For a function with ‘n’ input variables, the map requires 2^n cells. The arrangement of cells follows a specific pattern to facilitate the identification of adjacent terms:

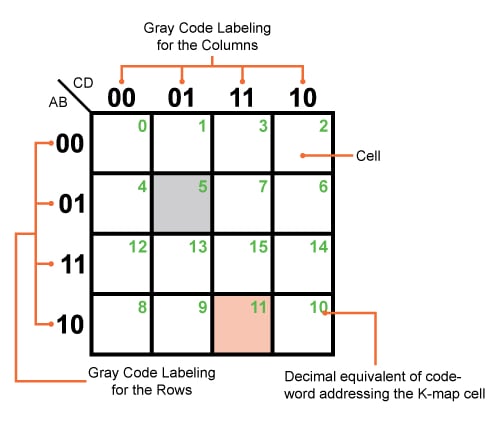
• Rows and Columns: The rows and columns of the map represent the different combinations of input variables. The order of variables in the rows and columns is crucial, adhering to the Gray code sequence, where only one bit changes between consecutive values. This ensures that adjacent cells differ in only one input variable.
• Cell Values: Each cell in the K-map represents a unique combination of input variables. The value within the cell corresponds to the output of the Boolean function for that specific input combination. Typically, a ‘1’ represents a ‘true’ output and a ‘0’ represents a ‘false’ output.

The Art of Simplification: Grouping Terms on a K-map

The key to using K-maps lies in identifying groups of adjacent cells containing ‘1’s. These groups represent common terms in the Boolean expression, allowing for simplification. The rules for grouping are as follows:

• Adjacent Cells: Cells are considered adjacent if they share a common edge, even if they are on opposite sides of the map. This is because of the wrapping nature of the map, where the first and last columns/rows are considered adjacent.
• Group Size: Groups can be formed of any size, but they must be a power of 2 (1, 2, 4, 8, etc.). Larger groups lead to simpler terms in the minimized expression.
• Maximum Coverage: The goal is to cover all ‘1’ cells with the fewest possible groups, aiming for the largest possible groups.
• Non-overlapping Groups: Groups should not overlap, although they can touch at a single corner.

Deriving the Simplified Expression

Once the groups are identified, the minimized Boolean expression can be derived by following these steps:

1. Identify the variables: Determine the input variables that remain constant within each group.
2. Form the product term: For each group, create a product term by ANDing the variables that are constant within the group.
3. Combine the product terms: Combine the product terms for all the groups using OR operators.

Example: Simplifying a Boolean Function with a K-map

Let’s consider the Boolean function F(A, B, C) = Σ(0, 1, 2, 3, 5, 7). This function represents a circuit with three input variables (A, B, C) and outputs a ‘1’ for the input combinations represented by the minterms 0, 1, 2, 3, 5, and 7.

1. Construct the K-map: Create a 3-variable K-map, with rows representing AB and columns representing C.
2. Populate the map: Place ‘1’s in the cells corresponding to the minterms (0, 1, 2, 3, 5, 7).
3. Identify groups: Identify the largest possible groups of adjacent ‘1’ cells. In this case, we can form two groups: one covering minterms 0, 1, 2, 3, and another covering minterms 5, 7.
4. Derive the simplified expression:
   • Group 1: The variables A and B are constant within this group, and C varies. Therefore, the term for this group is A’B’.
   • Group 2: The variables A and C are constant within this group, and B varies. Therefore, the term for this group is AB.
5. Combine the terms: The simplified expression is F(A, B, C) = A’B’ + AB.

Benefits of Using Karnaugh Maps

• Simplified Boolean Expressions: K-maps offer a systematic approach to minimizing Boolean expressions, leading to simpler and more efficient circuits.
• Visual Clarity: The graphical representation of the Boolean function provides a clear and intuitive understanding of the relationships between input variables and output values.
• Efficient Design Optimization: By simplifying expressions, K-maps enable the design of circuits with fewer logic gates, reducing cost, power consumption, and complexity.
• Error Detection: The visual nature of K-maps aids in identifying potential errors in the initial Boolean expression or in the grouping process.

Applications of Karnaugh Maps

K-maps find extensive applications in various fields:

• Digital Circuit Design: Simplifying Boolean expressions for logic gates, minimizing the number of gates required for a specific function.
• Computer Architecture: Optimizing the design of logic circuits within microprocessors and other digital systems.
• Control Systems: Designing control logic for industrial processes and automated systems.
• Data Processing: Simplifying expressions for data manipulation and filtering.

FAQs: Addressing Common Questions about Karnaugh Maps

Q1: What is the maximum number of variables that can be represented by a K-map?

A: While K-maps can be used for a limited number of variables, their effectiveness diminishes beyond five variables. For larger functions, other simplification techniques like Quine-McCluskey or algebraic manipulation are preferred.

Q2: How do I handle "don’t care" conditions in a K-map?

A: "Don’t care" conditions occur when the output of a function is irrelevant for specific input combinations. These conditions are represented by ‘X’ in the K-map. During grouping, ‘X’ cells can be included or excluded as needed to form larger groups and simplify the expression.

Q3: Can K-maps be used for functions with multiple outputs?

A: While K-maps are typically used for single-output functions, they can be extended to handle multiple outputs. This involves creating separate K-maps for each output, with the same input variables.

Q4: What are the limitations of using Karnaugh maps?

A: K-maps are effective for simplifying Boolean expressions with a limited number of variables. Their complexity increases rapidly with the number of inputs, making them less practical for functions with six or more variables.

Tips for Effective K-map Usage

• Start with a clear understanding of the Boolean function: Ensure you have a correct and complete representation of the function before constructing the K-map.
• Use the Gray code sequence for rows and columns: This ensures that adjacent cells differ in only one variable.
• Identify the largest possible groups: Prioritize larger groups to achieve the most simplified expression.
• Don’t forget the wrapping nature of the map: Remember that the first and last columns/rows are considered adjacent.
• Use "don’t care" conditions strategically: Include or exclude ‘X’ cells to form larger groups and simplify the expression.

Conclusion

Karnaugh maps serve as a valuable tool in the realm of digital circuit design, offering a visual approach to simplifying Boolean expressions and optimizing circuit design. Their ability to efficiently identify common terms and minimize expressions makes them indispensable for creating efficient and cost-effective digital systems. While their effectiveness may diminish with larger functions, K-maps remain a powerful technique for understanding and manipulating Boolean logic, contributing significantly to the advancement of digital technology.

Closure

Thus, we hope this article has provided valuable insights into Demystifying Karnaugh Maps: A Visual Approach to Boolean Logic Simplification. We hope you find this article informative and beneficial. See you in our next article!